By Joanna McKay & Vanessa Rayner

Despite the challenges of getting started (technical issues and bad weather were not on our side!) this was an amazing start to this two-part webinar series with Dr. Barbara Dougherty.
We started the session strong with Vanessa Rayner, PhD, a math consultant from Sir Wilfrid Laurier School Board as she introduced us to Assisting Students Struggling with Mathematics: Intervention in the Elementary Grades Educator’s Practice Guide and reviewed the Six Recommendations based on high-quality evidence-based research studies focused on Tier 1 mathematics instruction:
(Fuchs, L.S., Newman-Gonchar, R., Schumacher, R., Dougherty, B., Bucka, N., Karp, K.S., Woodward, J., Clarke, B., Jordan, N. C., Gersten, R., Jayanthi, M., Keating, B., and Morgan, S. (2021). Assisting Students Struggling with Mathematics: Intervention in the Elementary Grades (WWC 2021006). Washington, DC: National Center for Education Evaluation and Regional Assistance (NCEE), Institute of Education Sciences, U.S. Department of Education. Retrieved from http://whatworks.ed.gov/.)
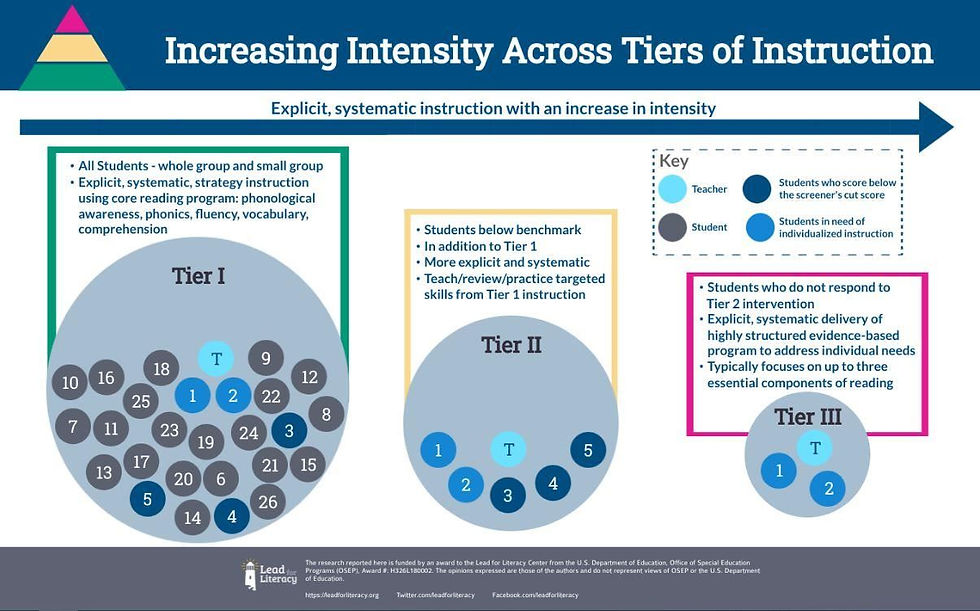
If your school is using a Multi-Tiered System of Supports (MTSS) model= Response to Intervention (RTI) + Positive Behaviour and Intervention Supports (PBIS), Tier 1 instruction is for everyone with about 80% of students achieving grade level standards. Tier 2 is systematic and planned based on goals that target building foundational skills over 5-10 days to achieve grade level content. Tier 3 is provided to students who require a more highly structured evidence-based program in addition to what was provided in Tier 2. Both Tier 2 & 3 offer intentional and systematic support that provides foundational learning. Remember depending on students' needs it could take 1-7+ exposures or practice with the same concept to "get it".

The Always Sometimes Never task opened the discussion on the importance of modeling the use of clear and concise mathematical language (Recommendation 2) to help students effectively communicate their understanding of math concepts. Barb, Karen Karp (another gem by Ms. Karp here), and Sarah Bush wrote a book called the Math Pact, which highlights how to achieve this in a school wide context as well as how to avoid using Rules That Expire:
Systematic instruction (Recommendation 1) is carefully designed instructional sequences that integrate the appropriate learning progressions. When we show students how old concepts pave the way to understand new concepts and procedures we build connections (between the small blue dots and the big red dot), which is KEY to understanding the mathematics we learn.
Not only did we see how conceptual understanding supports procedural knowledge from the video clip, we also began to explore how it is critical that fundamental concepts (such as the unit) are connected to and support several key concepts introduced at every cycle. Understanding the unit is tied to counting and place value (Cycle 1), fractions (Cycle 2), multiplicative reasoning (Cycle 3) and proportional reasoning (secondary Cycle 1). Being able to trace where a foundational concept was not adequately developed, helps us understand where we need to start to move student thinking forward. It also highlights the idea that, at all grade levels, we must use and make connections between the Concrete Semi-concrete Abstract representations (Recommendation 3).
Finally, we cannot forget how we got the session started with Barb using the Problem of Nines! Rich tasks like the Problem of Nines help reinforce arithmetic but do so much more! We were all engaged, and, without being prompted, looked for patterns to help us find all possibilities. Looking for patterns is a skill that benefits all of our students short- and long-term.
Choosing to integrate these tasks is only one piece of the puzzle. We need all students in the general education classroom to work together to establish a math community- focus on problems where the solution is to share and listen to different ways of thinking about mathematics. Rather than start the year with a review of last year’s content, why not get students ready for the mathematics they will learn and by using engaging problems that establish routines and community.
For more ideas check out:

Comments